Introduction
비정형데이터분석 과목을 수강하며 공부한 내용을 정리하는 포스팅입니다.
해당글은 순천향대학교 빅데이터공학과 우지영 교수님이 진행하시는 "비정형데이터분석" 강의를 기반으로 작성되었습니다.
지난 포스팅에 이어서 오늘은 퍼짐 정도(dispersion)에 대해서 알아보도록 하겠습니다.
퍼짐 정로란 무엇일까요?? 단어에서도 느껴지듯이 자료가 얼마나 퍼져있는지 얼마나 모여있고, 얼마나 흩어져 있는지 등을 의미합니다.
이 퍼짐 정도를 나타내주는 대표적인 통계치들에 대해 알아보도록 하겠습니다.
퍼짐 정도(dispersion)
(1) 분산
분산은 평균에 대한 편차 제곱의 평균을 구한 값
먼저 편차는 평균과의 차이를 의미합니다. 그렇기 때문에 편차의 합은 0이 됩니다. 그렇기 때문에 분산을 구하기 위해서는 편차를 그냥 더하는 것이 아닌 제곱을 더해서 구하는 것입니다.
분산의 의미는 만약 데이터가 평균에 가깝다면?? 편차는 작아지기 때문에 분산은 작아지고, 반대로 평균과 멀리 떨어져 있다면?? 편차는 커지기 때문에 분산 역시 증가하게 됩니다.
(2) 표준편차
표준편차는 분산의 양의 제곱근
표준편차의 정의는 다음과 같습니다. 분산이랑 비슷해 보이는데 표준편차는 왜 필요할까요??
우리는 분산에서 편차를 제곱하게 되면서 값이 크게 증가하는 경향이 있습니다. 그렇기 때문에 이 분산값으로는 데이터의 퍼짐을 파악하기는 살짝 어려운 경향이 있습니다.
따라서 제곱으로 인해 커지게된 분산의 값을 다시 루트를 적용함으로써 원래의 값으로 맞춰주는 것이지요.
(3) 변이계수(=변동계수)
변동 계수는 표준 편차를 산술 평균으로 나눈 값
변동 계수는 표준 편차를 표본 평균이나 모 평균 등 산술 평균으로 나눈 값입니다.
이 값은 보통 서로 다른 아이템들의 편차를 비교하기 위해서 사용이 된다고 합니다.
(4) 범위
범위는 최대값에서 최소값을 뺀 값
범위는 우리가 가장 이해하기 쉬운 퍼짐 정도를 나타내는 통계량입니다.
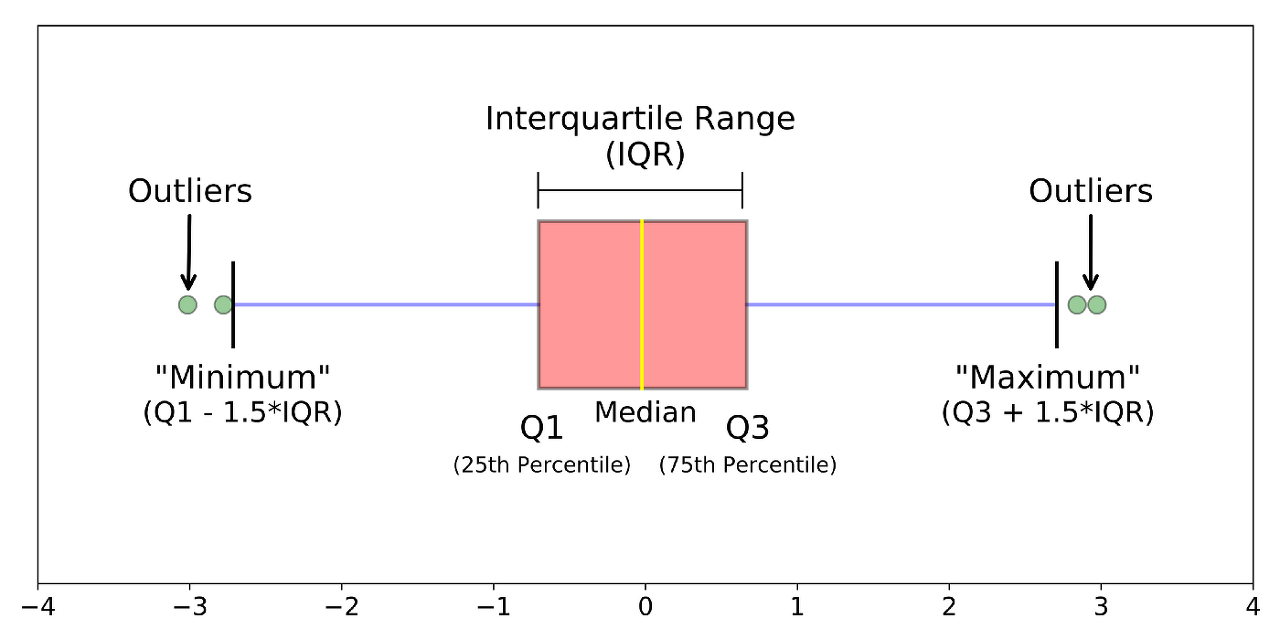
하지만 범위에는 단점이 있습니다. 바로 특이값에 민감하다는 점입니다. 그게 무슨말이냐 하면 위 그래프와 같이 데이터가 분포한다고 했을때 범위값을 구하게 되면 과연 이 값이 이 자료의 범위를 잘 표현할 수 있을까요??
아닙니다. 왜냐하면 그림에서 보이듯이 최솟값과 최댓값은 매우 특이한 즉, 이상치값으로 존재하게 됩니다. 따라서 이 데이터의 범위에서는 살짝 벗어난 값들로 나타나게 됩니다. 이러한 범위의 단점을 커버한 값이 바로 IQR입니다.
(5) IQR
IQR은 3분위수에서 1분위수를 뺀 값
그림에서 보면 분홍색 박스 부분이 IQR값을 의미하는데 이 값은 범위와 달리 특이값에 견고하기 때문에 범위보다 더 적합한 통계치를 추출할 수 있습니다.
(6) 백분위수
자료의 수가 n개 일 때, 제 100 x p 의 백분위 수는 그 값보다 작거나 같은 관측값의 개수가 np개 이상, 그 값보다 크거나 같은 관측값이 n(1-p)개 이상인 값
(7) 사분위수
사분위수는 데이터 표본을 4개의 동일한 부분으로 나눈 값
- 제 1사분위수(Q1) - 25 백분위수
- 제 2사분위수(Q2) - 50 백분위수
- 제 3사분위수(Q3) - 75 백분위수
우리가 데이터의 특징을 파악할때 많이 사용하는 Boxplot이 바로 이 사분위수의 값을 시각화를 통해 표현한 값입니다.
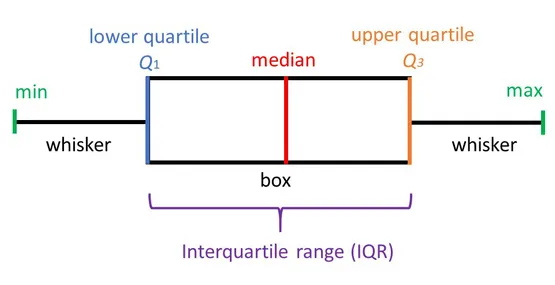
Boxplot 각각의 의미는 다음과 같습니다.
- min : 제 1사분위에서 1.5 IQR1을 뺀 위치입니다.
- 제 1사분위(Q1) : 25%의 위치를 의미합니다.
- 제 2사분위(Q2) : 50%의 위치로 중앙값(median)을 의미합니다.
- 제 3사분위(Q3) : 75%의 위치를 의미합니다.
- 최댓값 : 제 3사분위에서 1.5 IQR을 더한 위치입니다.
다음은 R에서 제공하는 퍼짐 정도와 관련된 함수들입니다.
| 산술통계 | 통계량 | R function |
| 퍼짐 정도 (dispersion) |
분산 | var() |
| 표준편차 | sd() | |
| 변이계수 | 100*sd(x)/mean(x) | |
| 범위 | diff(range()) | |
| IQR | IQR(): 값 하나로 나옴 | |
| 최소값 | min() | |
| 최대값 | max() | |
| 백분위수 | quantile(x, probs=c(,,,,)) |
참고
rfriend.tistory.com/121
dschloe.github.io/python/python_edu/03_datavisualisation/ch_boxplot/
'비정형데이터분석' 카테고리의 다른 글
| [비정형 데이터 분석] 변화 분석 (0) | 2021.04.07 |
|---|---|
| [비정형 데이터 분석] Peak로 특징 찾기 (0) | 2021.03.24 |
| [비정형 데이터 분석] 분포형태와 대칭정도(distribution, symmetry) (0) | 2021.03.23 |
| [비정형 데이터] 중심화 경향 값 (0) | 2021.03.21 |
| [비정형 데이터 분석] 비정형 데이터란? (0) | 2021.03.03 |


