Introduction
비정형데이터분석 과목을 수강하며 공부한 내용을 정리하는 포스팅입니다.
해당글은 순천향대학교 빅데이터공학과 우지영 교수님이 진행하시는 "비정형데이터분석" 강의를 기반으로 작성되었습니다.
지난 포스팅에 이어서 오늘은 분포형태와 대칭정도(distribution)에 대해서 알아보도록 하겠습니다.
분포형태와 대칭정도(distribution)
(1) 왜도(Skewness)
실수 값 확률 변수의 확률 분포 비대칭성을 나타내는 지표
정규분포 또는 t분포처럼 대칭인 분포들은 왜도가 0이게 됩니다. 대칭이 아니면 왜도의 값은 어떻게 달라질까요?
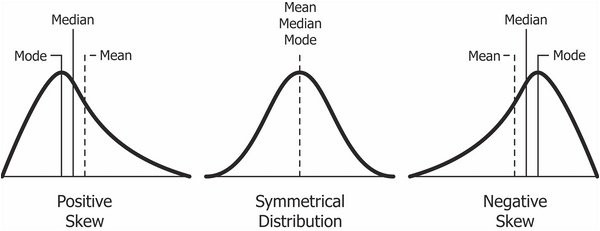
왜도에는 다음과 같이 Postive Skew, Negativw Skew 두가지 종류가 있습니다. 보통 오른쪽으로 꼬리가 긴, 왼쪽으로 꼬리가 긴이라고 많이 불립니다.
Postive Skew: 양의 왜도는 오른쪽으로 꼬리가 길게 분포해있으며 평균값은 중앙값과 최빈값보다 큰 값을 가지게 됩니다.
Negative Skew: 음의 왜도는 왼쪽으로 꼬리가 길게 분포해 있으며 평균값은 중앙값과 최빈값보다 작은 값을 가지게 됩니다.
(2) 첨도(kurtosis)
첨도는 확률분포의 뾰족한 정도를 나타내는 척도
관측치들이 어느 정도 집중적으로 중심에 몰려 있는가를 측정할 때 사용이 됩니다.
또한 첨도를 통해 이상치에 대해서도 판별을 할 수 있습니다. 얼마나 극단한 값을 가지는지!!
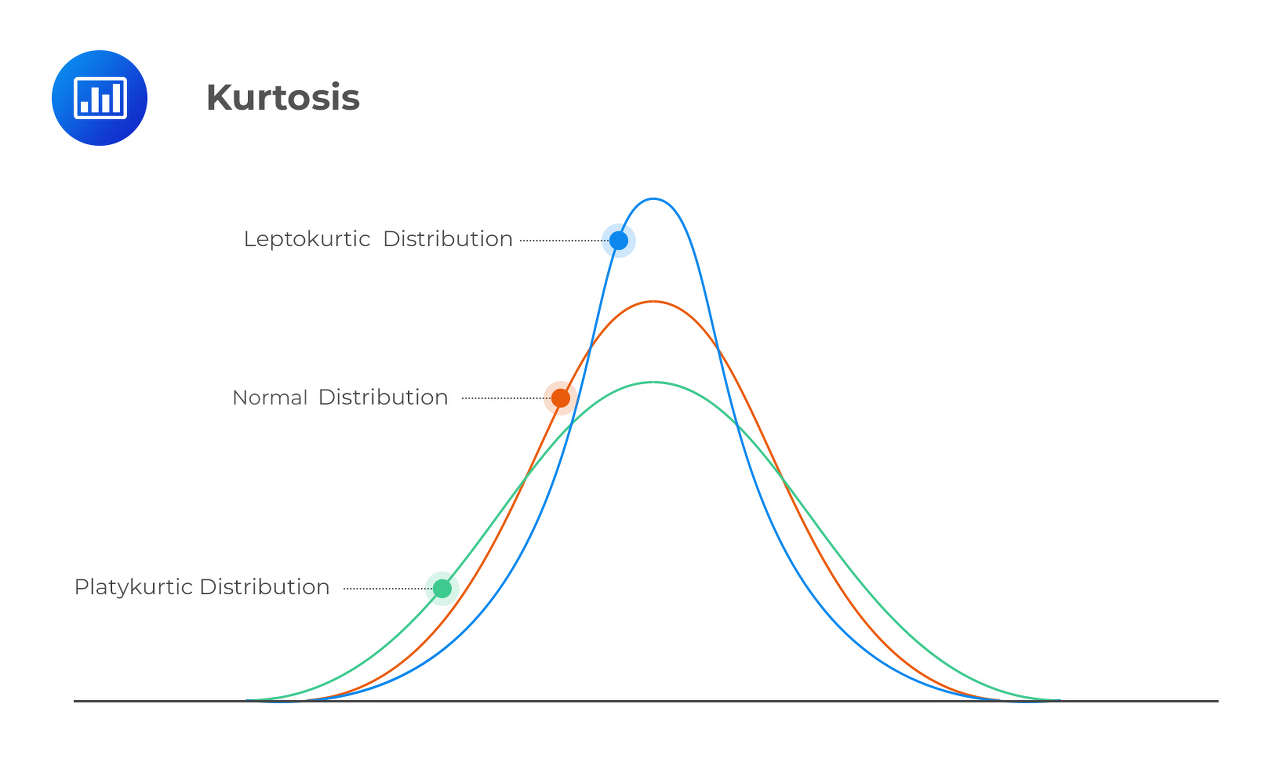
정규분포의 첨도는 0입니다. (기본적인 정의에 의하면 3이라고도 하는데 일반적으로 정규분포의 첨도를 0으로 만들기 위해서 3을 빼서 정의하는 경우가 많다고 합니다.)
Leptokurtic: 첨도가 0보다 크면 정규분포보다 긴 꼬리를 가지게 됩니다. 이 경우는 데이터들이 지나치게 평균에 밀집되어 있다고 해석할 수 있습니다.
Platykurtic: 첨도가 0보다 작으면, 정규분포보다 짧은 꼬리를 가지게 됩니다. 이 경우는 데이터들이 정규분포를 이룰 만큼 평균에 밀집되어 있지 않다고 해석할 수 있습니다.
(3) 분위수-분위수(Q-Q plot)
정규분포일때의 이론적 분위수와 표본의 실제 분위수를 비교하는 것
Q-Q plot은 정규모집단 가정을 하는 방법 중 하나로 표준정규분포의 분위수와 비교하여 그리는 그래프입니다.
Q-Q plot을 사용할때는 주로 우리가 가지고 있는 데이터와 정규분포를 비교합니다. 따라서 '정규성 검정'의 한 방법이라고도 말할 수 있습니다.
Q-Q plot 예시는 다음과 같습니다.
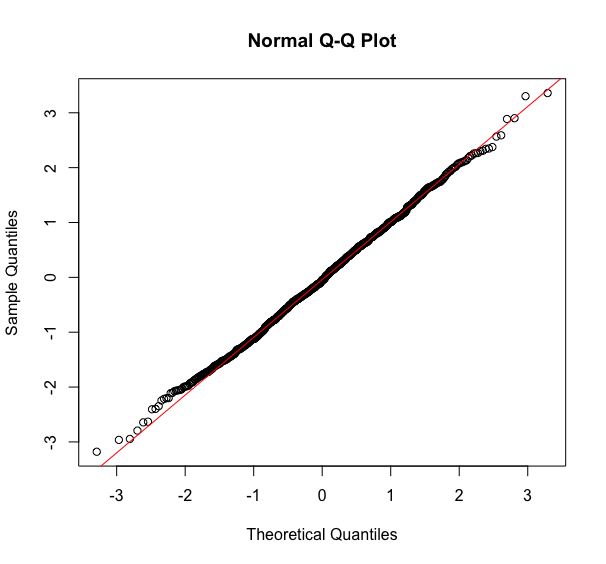
그래프를 그렸을때 표본이 정규분포를 따른다면 직선의 형태로 보이게 됩니다. 반면에 정규분포에서 벗어나는 값을 가지면 여러가지 비선형 형태로 보이게 됩니다.(ex. S or 바나나 모양)
다음 그래프는 정규분포를 만족한다고 말할 수 있습니다. 하지만 이 Q-Q plot을 해석하는 과정에서는 주관적이기 때문에 사람들마다 차이가 있다. 따라서 다른 검정값들도 같이 비교하면서 확인을 해야 좀 더 정확한 판단을 할 수 있겠습니다.
다음은 R에서 제공하는 분포형태, 대칭정도와 관련된 함수입니다.
| 산술통계 | 통계량 | R function |
| 분포형태와 대칭정도 (distribution, symmetry) |
왜도 | rowSkewness(), fBasics packages |
| 첨도 | rowKurtosis(), fBasics packages | |
| 분위수-분위수 | qqnorm(), qqline(), qqplot() |
참고
analystprep.com/cfa-level-1-exam/quantitative-methods/kurtosis-and-skewness-types-of-distributions/
Kurtosis and Skewness Example Question | CFA Level I - AnalystPrep
Kurtosis refers to a measure of the degree to which a given distribution is more or less ‘peaked’, relative to the normal distribution
analystprep.com
'비정형데이터분석' 카테고리의 다른 글
| [비정형 데이터 분석] 변화 분석 (0) | 2021.04.07 |
|---|---|
| [비정형 데이터 분석] Peak로 특징 찾기 (0) | 2021.03.24 |
| [비정형 데이터 분석] 퍼짐 정도(dispersion) (0) | 2021.03.23 |
| [비정형 데이터] 중심화 경향 값 (0) | 2021.03.21 |
| [비정형 데이터 분석] 비정형 데이터란? (0) | 2021.03.03 |


