회귀 모델은 데이터에 적합하면서도 회귀 계수가 기하급수적으로 커지는 것을 제어할 수 있어야 합니다. 선형 모델의 비용함수를 RSS를 최소화하는 즉 실제 값과 예측값의 차이를 최소화하는 것만 고려하게되면 학습 데이터에 지나치게 맞추어지고 회귀 계수가 쉽게 커지게 됩니다. 이를 개선하기 위해서 비용 함수는 학습 데이터의 잔차 오류 값을 최소로 하는 RSS값을 최소로 하는 방법과 과적합 방지를 위해서 회귀 계수의 값이 커지지 않게 서로 균형을 이루도록 하는것이 중요합니다.
이것을 수식으로 표현하면 다음과 같이 표현할 수 있습니다.
$$Min(RSS(W) + alpha * ||W||^2_{2})$$
수식을 해석하면 alpha는 학습 데이터의 적합 정도와 회귀 계수 값의 크기를 제어해주는 튜닝 파라미터입니다.
alpha가 0이라고 한다면 비용 함수의 식은 Min(RSS(W)+0)이 됩니다. 반면에 alpha가 무한대라고 한다면 비용함수 식은 RSS(W)에 비해서 alpha*||W||제곱의 값이 너무 커지기 때문에 W 값을 0으로 만들어야 Cost가 최소화되는 비용 함수 목표를 달성할 수 있습니다.
다시 말하자면 alpha를 0에서부터 증가시키면서 회귀 계수 값의 크기를 감소시킬 수 있습니다. 이렇게 비용 함수에 alpha값을 통해서 패널티를 부여해 회귀 계수의 값 크기를 감소시키면서 과적합을 개선해 나가는 방식을 규제(Regularization)이라고 합니다.
규제는 L2방식과 L1 방식으로 나눌 수 있습니다. L2 규제 방식은 W의 제곱에 대해 패널티를 부여하는 방식을 말하고 릿지 회귀라고 합니다. L1 규제는 W의 절댓값에 대해 패널티를 부여하는 방식으로 라쏘 회귀라고 합니다.
릿지 회귀
사이킷런에서는 Ridge 클래스를 통해서 릿지 회귀를 구현할 수 있습니다. 주택 가격 데이터를 사용해서 Ridge 클래스를 이용해 예측을 해보도록 하겠습니다.
from sklearn.linear_model import Ridge
from sklearn.model_selection import cross_val_score
ridge = Ridge(alpha=10) # alphq 10으로 설정
neg_mse_score = cross_val_score(ridge, X_data, y_target, scoring="neg_mean_squared_error",cv=5)
rmse_score = np.sqrt(-1*neg_mse_score)
avg_rmse = np.mean(rmse_score)print('Negative MSE:',np.round(neg_mse_score,3))
print('RMSE:',np.round(rmse_score,3))
print('평균 RMSE:{0:.3f}'.format(avg_rmse))
규제가 없이 그냥 LinearRegression을 적용했을때보다 더 뛰어난 예측 성능을 보여주게 되는 것을 알게되었습니다.
다음은 alpha값을 변화시키면서 RMSE 값이 어떻게 변화하는지 살펴보도록 하겠습니다.
alphas = [0, 0.1, 1, 10, 100]
for alpha in alphas:
ridges = Ridge(alpha= alpha)
neg_mse_score = cross_val_score(ridges, X_data, y_target, scoring="neg_mean_squared_error",cv=5)
avg_rmse = np.mean(np.sqrt(-1*neg_mse_score))
print('alpha값{0}일 때의 평균 RMSE:{1:.3f}'.format(alpha,avg_rmse))
alpha가 100일 때 평균 RMSE가 가장 좋은 것을 확인하였습니다. 다음은 이부분을 시각화로 표현해 보도록 하겠습니다. 회귀 계수를 coef_속성을 통해 추출하고 Series 객체로 만들어서 막대 차트로 표현해 보도록 하겠습니다.
fig, axs = plt.subplots(figsize =(18,6), nrows=1, ncols=5)
coef_df = pd.DataFrame()
for state, alpha in enumerate(alphas):
ridges = Ridge(alpha=alpha)
ridges.fit(X_data, y_target)
coef = pd.Series(data=ridges.coef_, index= X_data.columns)
colname = 'alpha:'+str(alpha)
coef_df[colname] = coef
coef = coef.sort_values(ascending=False)
axs[state].set_title(colname)
axs[state].set_xlim(-3,6)
sns.barplot(x=coef.values, y=coef.index,ax=axs[state])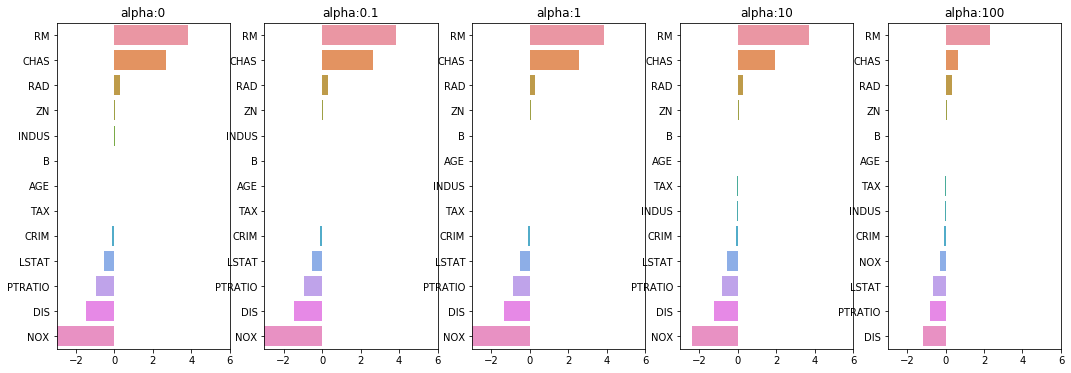
NOX 피처를 보면 alpha 값이 증가하면서 회귀 계수가 크게 작아지는 것을 확인할 수 있습니다.
다음은 데이터프레임에 저장된 릿지 회귀 계수의 값입니다.
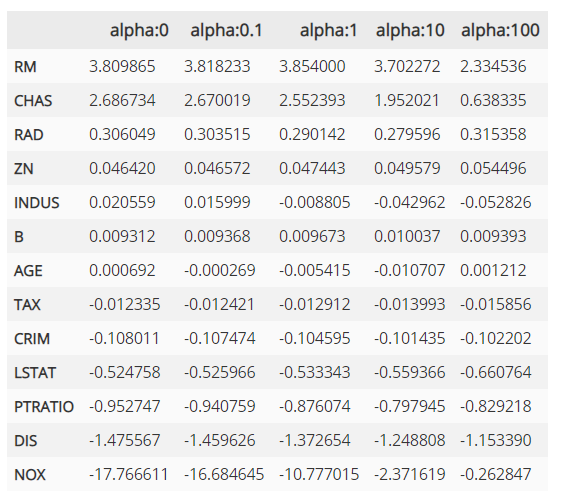
라쏘 회귀
L2 규제가 회귀 계수의 크기를 감소시키는데 반해 L1 규제는 불필요한 회귀 꼐수를 급격하게 감소시켜서 0으로 만들고 제거하여 줍니다. 따라서 L1 규제는 적절한 피처들만 회귀에 포함시키는 피처 선택의 특징을 가지고 있습니다.
사이킷런에서는 Lasso 클래스를 사용해서 라쏘 회귀를 구현할 수 있습니다. 알파값은 [0.07, 0.1, 0.5, 1, 3]으로 변화하도록 하겠습니다.
from sklearn.linear_model import Lasso
Lasso_alphas = [0.07, 0.1, 0.5, 1, 3]
for alpha in Lasso_alphas:
ridges = Lasso(alpha= alpha)
neg_mse_score = cross_val_score(ridges, X_data, y_target, scoring="neg_mean_squared_error",cv=5)
avg_rmse = np.mean(np.sqrt(-1*neg_mse_score))
print('alpha값{0}일 때의 평균 RMSE:{1:.3f}'.format(alpha,avg_rmse))
alpha값이 0.7일 때 가장 좋은 결과가 나왔습니다. 앞의 릿지 회귀의 평균보다는 떨어지는 결과가 나왔습니다.
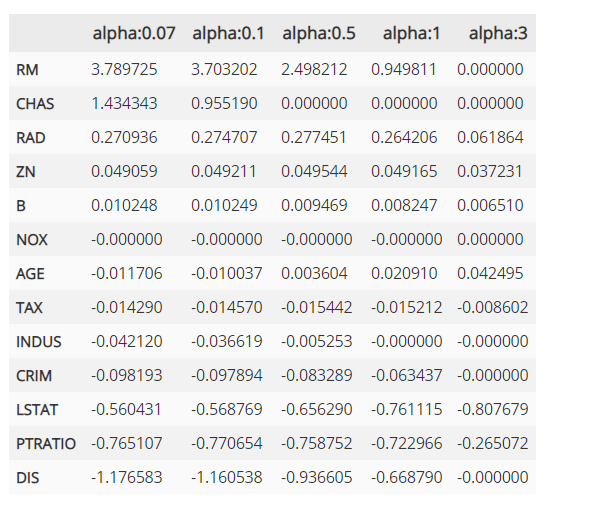
회귀계수의 값을 보면 alpha가 증가함에 따라서 일부 피처들의 회귀 계수가 0으로 바뀌는 것을 알 수 있습니다.
NOX 피처는 alpha가 0.07일때 부터 회귀 계수가 0이고 몇개의 피처들은 alpha가 증가하면서 회귀 계수가 0으로 바뀌게 됩니다. 이렇게 회귀 계수가 0인 피처는 회귀 식에서 제외되면서 피처 선택의 효과를 얻게 되는 것입니다.
엘라스틱넷 회귀
엘라스틱넷 회귀는 L2규제와 L1규제를 결합한 회귀 방식입니다. 엘라스틱넷은 라쏘 회귀가 서로 상관관계가 높은 피처들의 경우에서 중요 피처들을 선택하고 다른 피처들은 모두 0으로 만드는 성향이 강합니다. 특이 이러한 이유로 alpha값에 따라 회귀 계수의 값이 급격하게 변할수 있는데 엘라스텍 회귀는 이를 개선하기 위해서 L2 규제를 라쏘 회귀에 추가한 것입니다. 하지만 아무래도 결합된 규제이기 때문에 시간이 오래걸린다는 단점이 있습니다.
사이킷런에서는 ElasticNet 클래스를 사용해서 엘라스틱넷 회귀를 구현할 수 있습니다. 엘라스틱의 규제는 a*L1 + b*L2로 정의합니다. 여기서 a는 L1의 알파값 b는 L2의 알파값을 의미합니다. 예제에서는 L1_ratio를 0.7로 고정하도록 하겠습니다.
from sklearn.linear_model import ElasticNet
elastic_alphas = [0.07, 0.1, 0.5, 1, 3]
for alpha in elastic_alphas:
elastic = ElasticNet(alpha= alpha, l1_ratio=0.7)
neg_mse_score = cross_val_score(elastic , X_data, y_target, scoring="neg_mean_squared_error",cv=5)
avg_rmse = np.mean(np.sqrt(-1*neg_mse_score))
print('alpha값{0}일 때의 평균 RMSE:{1:.3f}'.format(alpha,avg_rmse))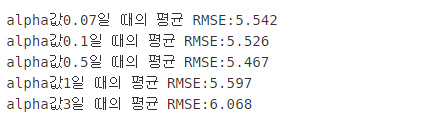
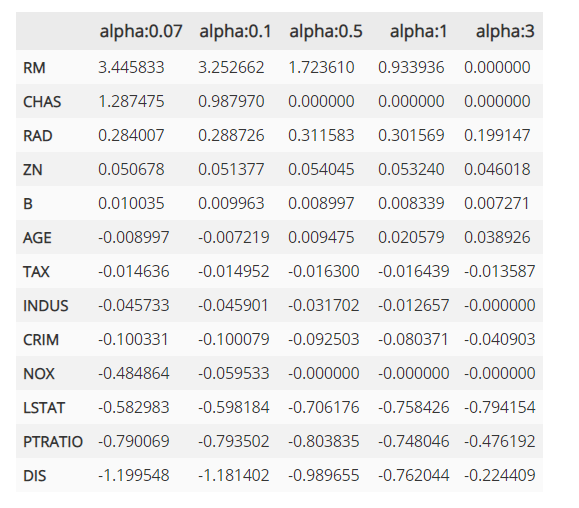
alpha값에 따른 피처들의 회귀 계수들을 봤을때 라쏘의 결과보다 0이 되는 값이 적은것을 알 수 있습니다. 데이터에 따라서 어떤 규제를 적용하면 좋을지 하이퍼 파라미터를 잘 조절해 가면서 최적의 예측 성능을 찾아야 합니다. 하지만 선형 회귀ㅇ는 먼저 데이터의 분포도의 정규화와 인코딩 방법이 매우 중요하다고 합니다!!
Reference
'Machine Learning' 카테고리의 다른 글
| 회귀 평가 지표 (0) | 2020.05.27 |
|---|---|
| 로지스틱 회귀 (2) | 2020.05.27 |
| LinearRegression 실습( 주택 가격 예측) (0) | 2020.05.27 |
| 회귀란? (0) | 2020.05.26 |
| ML 평가 지표 (0) | 2020.05.09 |


