고유값과 고유벡터
선형변환 A에 의한 변환 결과가 자기 자신의 상수배가 되는 0이 아닌 벡터를 고유벡터라고 하고 이 상수배의 값을 고유값이라고 합니다.
다시 말하자면 n X n 정방행렬 A에 대해 Av = λv를 만족하는 0이 아닌 열벡터 v를 고유벡터, 상수 λ를 고유값이라 정의합니다. (고유값, 고유벡터는 정방행렬에 대해서만 정의합니다.)
- 정방행렬: 열과 행의 개수가 동일한 행렬을 정방 행렬이라고 합니다.
추가 설명을 하자면 먼저 선형 변환은 벡터에 사칙연산을 해주겠다! 라고 생각하면 됩니다. Av = λv를 보고 설명을 해보면 벡터 v에 행렬 A를곱하는 것을 '벡터 v에 선형 변환 A를 해주었다.'라고 이야기 할 수 있습니다.
그렇다는 것은 Av는 v벡터에 선형 변환 A를 해주었다는 뜻이겠죠?? v라는 벡터에 선형 변환 A를 해준 결과와 벡터 v의 상수 배(λ)와 동일하게 된다면?? 그게 바로 '선형 변환 A에 대하여 v는 고유 벡터, λ는 고유값이다'라고 하게 되는 것입니다.
Av = λv 를 만족하면 벡터 v의 방향은 변하지 않고 크기만 변했다는 뜻입니다.
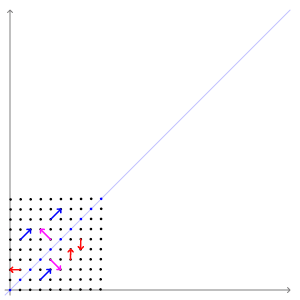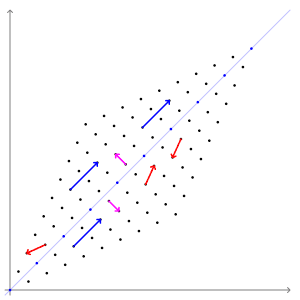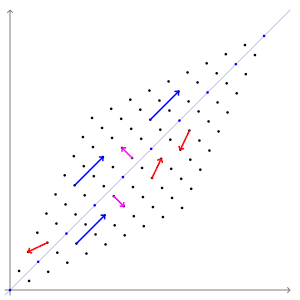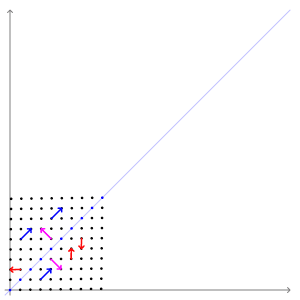
위의 예시를 선형변환의 예시입니다. 빨간색 벡터를 보면 벡터의 방향과 크기가 모두 변하였습니다. 그렇기 때문에 빨간색 벡터는 고유 벡터라고 말할 수 없습니다. 파란색 벡터는 방향은 변함이 없고 크기만 변하는 것을 확인할 수 있습니다. 바로 이러한 벡터를 보고 고유 벡터라고 부르게 됩니다.
고유값은 (변환 후 파란색 벡터 크기 / 변환 전 파란색 벡터 크기)로 계산하게 됩니다.
고유값 분해
고유값 분해(eigen decomposition)는 교유값과 고유벡터로 부터 유도되는 고유값 행렬과 고유벡터 행렬에 의해서 분해될수 있는 행렬의 표현입니다.
선형 독립을 만족하는 정방행렬 A는 고유값 분해에 의해서 다음과 같이 분해됩니다.

여기서 P는 정방행렬 A의 고유벡터들을 열벡터로 가지는 행렬이고, Λ는 고유값을 대각원소로 가지는 대각행렬입니다.
한번 증명을 해보도록 하겠습니다.
선형 독립을 만족하는 정방행렬 A의 고유값과 고유벡터를 λi, 고유벡터를 vi, i = 1, 2,..., n이라고 하겠습니다.

고유값과 고유벡터의 정의에 의해서 정리를 하면 다음과 같이 식이 변형됩니다.
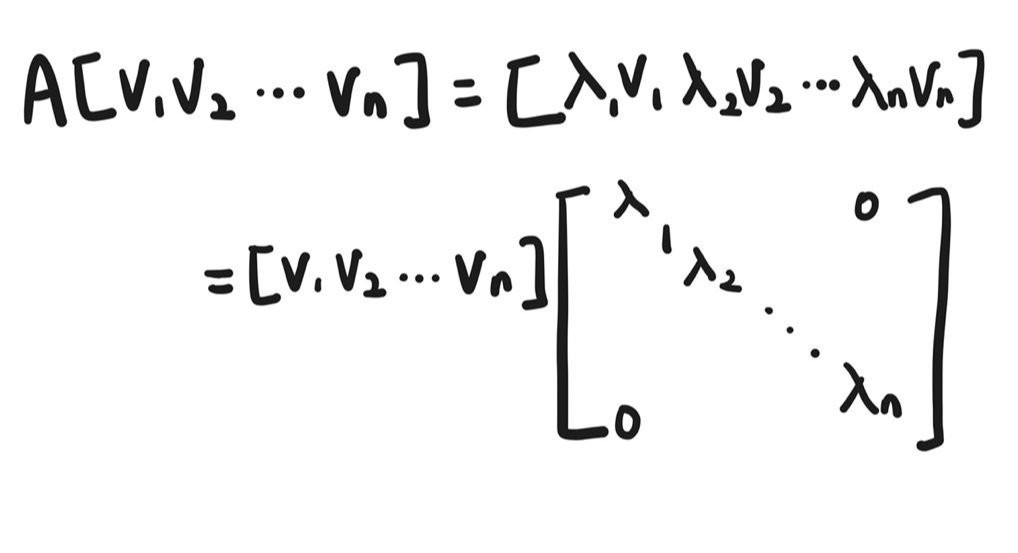
P: 행렬 A의 고유 벡터들을 열 벡터로 하는 행렬
Λ:고유값을 대각원소로 가지는 대각 행렬
라고 한다면 다음의 식이 성립하게 됩니다.
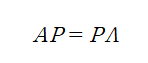

이것을 행렬 A에 대한 고유값 분해라고 합니다. 즉 P는 고유 벡터들을 열벡터로 하는 행렬이고, Λ는 고유값을 대각원소로 가지는 대각 행렬입니다.
Reference
1. https://ko.wikipedia.org/wiki/%EA%B3%A0%EC%9C%A0%EA%B0%92_%EB%B6%84%ED%95%B4
고유값 분해 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 둘러보기로 가기 검색하러 가기
ko.wikipedia.org
2. https://darkpgmr.tistory.com/105
[선형대수학 #3] 고유값과 고유벡터 (eigenvalue & eigenvector)
선형대수학에서 고유값(eigenvalue)과 고유벡터(eigenvector)가 중요하다고 하는데 왜 그런 것인지 개인적으로도 참 궁금합니다. 고유값, 고유벡터에 대한 수학적 정의 말고 이런 것들이 왜 나왔고 그
darkpgmr.tistory.com
'Machine Learning' 카테고리의 다른 글
| TF-IDF란? (0) | 2021.01.21 |
|---|---|
| 특이값 분해(Singular Value Decomposition, SVD) (0) | 2020.08.11 |
| 차원 축소(Dimension Reduction) (0) | 2020.06.17 |
| 회귀 실습 - (자전거 대여 수요 예측) (0) | 2020.05.28 |
| 회귀 실습 - (자전거 대여 수요 예측) (0) | 2020.05.28 |

