특이값 분해(Singular Value Decomposition, SVD)

고유값 분해는 정방 행렬에 대해서만 가능하다고 배웠습니다. 그렇다면 다른 행렬들은 분해를 못하는 걸까요??

 

아니요!! 바로 특이값 분해라는 것이 있는데요. 특이값 분해는 정방 행렬뿐만 아니라 행과 열의 크기가 다른 모든 직각 행렬에 적용을 할 수 있습니다.

 

특이값 분해

---

먼저 특이값 분해는 실수 벡터 공간에 한정하여서 설명합니다. 특이값 분해는 행렬 A가 m X n 행렬일때, 아래 수식과 같이 3개의 행렬의 곱으로 분해되는 것을 말합니다.

 

 

 

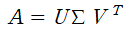
•  직교행렬: 자신과 자신의 전치 행렬의 곱 또는 이를 반대로 곱한 결과가 단위행렬이 되는 행렬
•  대각행렬: 주 대각선을 제외한 모든 원소가 모두 0인 행렬

 

1. 전치 행렬(Transposed Matrix)

---

전치 행렬은 행과 열을 교환하여서 얻은 행렬입니다. 다시 말하자면 주대각선을 축으로 하는 반사 대칭을 가하여 얻은 행렬입니다.

 

 

 

 

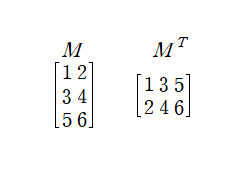
2. 단위 행렬(Identity Matrix)

---

단위 행렬은 주대각선의 원소가 1이고 나머지 원소는 모두 0인 정사각 행렬을 의미합니다.

 

 

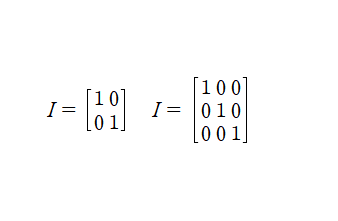
3. 역행렬(Inverse Matrix)

---

자신과 어떠한 행렬을 곱했을 때 나온 결과가 단위행렬이 나올때 그 행렬을 역행렬이라 합니다.

 

 

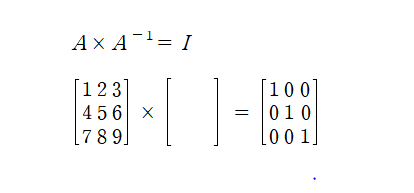
4. 직교 행렬(Orthogonal Matrix)

---

n x n 행렬 A에 대해서 A × A^T= I 를 만족하고 A^T x A = I 를 만족하는 행렬 A를 직교 행렬이라고 합니다.

 

5. 대각 행렬(Diagonal Matrix)

---

주대각선 성분이 아닌 모든 성분이 0인 정사각 행렬을 말합니다.

 

 

 

 

 

 

 

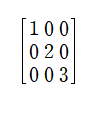
Reference

1) https://stementor.tistory.com/entry/%EC%84%A0%ED%98%95%EB%8C%80%EC%88%98%ED%95%9911%ED%96%89%EB%A0%AC%EC%9D%98-%EC%97%B0%EC%82%B0

선형대수학_1.행렬의 연산(1)

2)

https://ko.wikipedia.org/wiki/%EB%8B%A8%EC%9C%84%ED%96%89%EB%A0%AC

단위행렬 - 위키백과, 우리 모두의 백과사전