지도학습은 정답이 있는 데이터가 주어진 상황에서 학습하는 ML 알고리즘의 방식입니다.
지도학습의 대표적인 유형중 하나인 분류(Classfication)는 학습 데이터의 피처와 레이블값을 ML 알고리즘으로 학습하고, 학습한 모델에 새로운 값이 주여졌을 때 미지의 레이블 값을 예측하는 것입니다.
결정 트리란??
결정 트리(Decision Tree)는 ML 알고리즘 중에서 직관적으로 이해하기 쉬운 알고리즘입니다. 데이터에 있는 규칙을 학습을 통해서 자동으로 찾아내 트리 기반의 분류 규칙을 만드는 것입니다. 쉽게 비유를 하자면 스무고개와 유사한 방식으로 if, else를 기반으로 예측을 위한 규칙을 만든다고 생각하면 됩니다.
결정 트리에서는 데이터의 어떤 기준을 바탕으로 규칙을 만들어야 가장 효율적인 분류가 될가?? 가 알고리즘의 성능을 크게 좌우하게 됩니다.
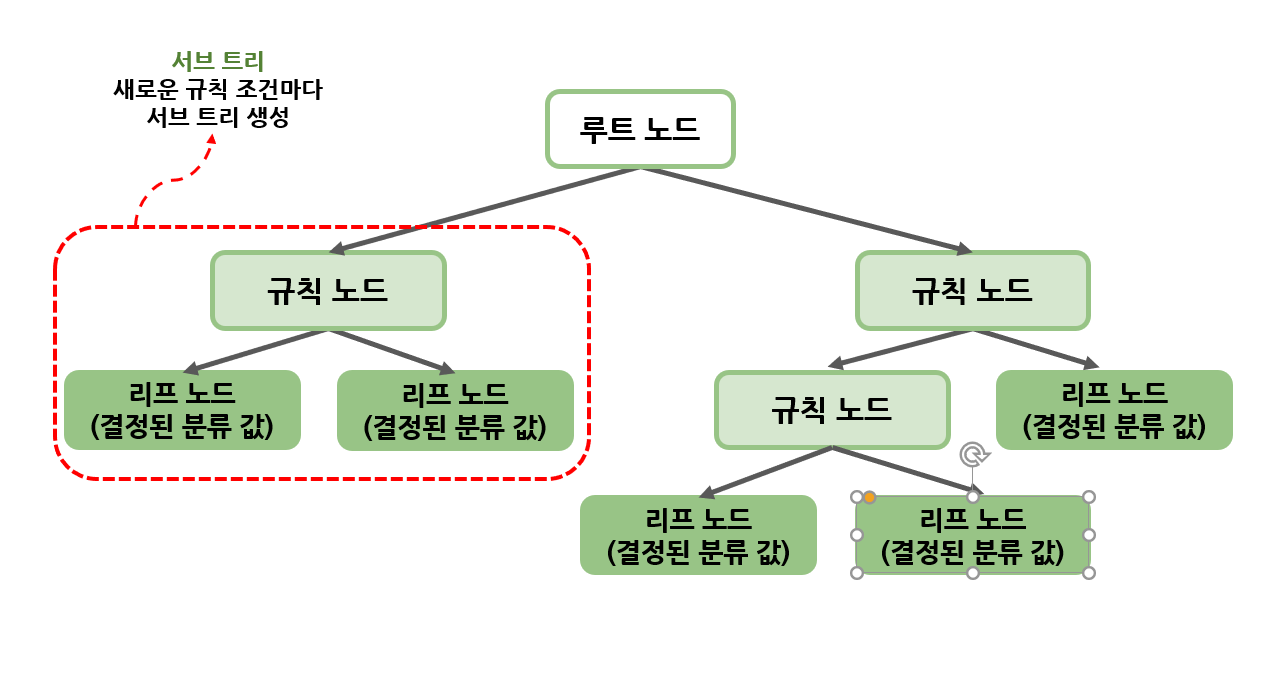
결정 트리는 다음과 같은 구조로 구성되어 있습니다. 데이터의 피처가 있고 이러한 피처들이 결합해 규칙 조건을 만들 때마다 규칙 노드가 만들어집니다. 하지만! 많은 규칙이 있다는것은 즉 분류를 결정하는 방식이 복잡해진다는 것을 의미합니다. 이는 과적합으로 이어지기 쉽습니다
정리하자면 트리의 깊이가 깊어질수록 결정 트리의 예측 성능이 저하될 가능성이 높습니다!
그렇다면 가능한 적은 결정 노드로 높은 정확도를 가질려면 어떻게 해야될까요??
정답은!! 최대한 많은 데이터 세트가 해당 분류에 속할 수 있도록 결정 노드의 규칙이 정해져야 한다는 것입니다.
그렇기 위해서는 트리를 분할 할때 최대한 균일한 데이터 세트를 구성하게 분할해야 합니다.
균일한 데이터란 무엇일까요??
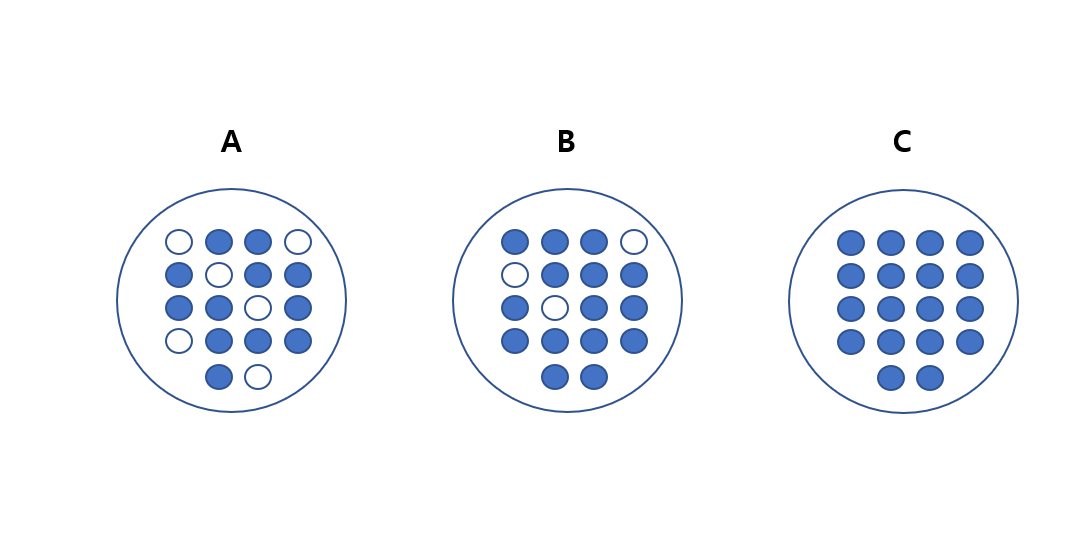
위 그림에서는 C > B > A 순으로 균일도가 높다고 할 수 있습니다. C는 모두 파란색 공으로 데이터가 모두 균일한 상태입니다. B의 경우는 일부의 하얀색 공을 가지고 있지만 대부분 파란색 공으로 구성되어 있어 C다음으로 균일도가 높습니다.
예를들어 눈을 가린 상태에서 C에서 하나의 공을 뽑았을때는 별다른 정보가 없어도 파란색 공이라는것을 알 수 있습니다. 하지만 A의 경우는 혼잔도가 높고 균일도가 낮기 때문에 공의 색깔을 판단하려면 많은 정보가 필요하게 됩니다.
이러한 데이터 세트에서 균일도는 데이터를 구분하는데 있어서 필요한 정보의 양에 영향을 미치게 됩니다.
정보의 균일도를 측정하는 대표적인 방법에는 엔트로피를 이용한 정보 이득(Information Gain)지수와 지니계수가 있습니다.
정보이득?
정보 이득은 엔트로피라는 개념을 기반으로 합니다. 엔트로피는 주어진 데이터 집합의 혼잡도를 의미합니다. 서로 다른 값들이 섞여 있으면 엔트로피가 높고, 같은 값이 섞여 있으면 엔트로피가 낮습니다. 정보 이득은 (1- 엔트로피) 로 계산합니다. 결정 트리는 정보 이득이 높은 속성을 기준으로 데이터를 분할합니다.
지니 계수?
지니 계수는 원래는 경제학에서 불평등 지수를 나타낼 때 사용되는 계수입니다. 지니 계수는 0이 가장 평등하고 1로 갈수록 불평등합니다. 결정 트리는 지니 계수가 낮을수록 데이터 균일도가 높은 것으로 해석해서 지니 계수가 낮은 속성을 기준으로 분할합니다.
결정 트리 모델의 특징
결정 트리의 가장 큰 장점은 정보의 "균일도"를 기반으로 하고 있어서 알고리즘이 쉽고 직관적이라는 점입니다. 정보의 균일도만 신경을 쓰면 되기 때문에 특별한 경우를 빼고는 전처리 작업(스케일링, 정규화)이 필요없습니다. 반면에 결정 트리의 가장 큰 단점은 바로 과적합으로 인한 정확도가 떨어진다는 점입니다.
결정 트리는 정확도를 높이기 위해서 계속 조건을 추가하고 트리의 깊이가 깊어지기 때문에 복잡한 모델이 만들어 질 수 밖에 없습니다. 복잡한 데이터는 새로운 데이터에 대한 대처 능력이 떨어져 결국 예측 성능이 떨어지게 됩니다.
결정 트리 파라미터
- DecisionTreeClassifier: 분류를 위한 클래스
- DecisionTreeRegressor: 회귀를 위한 클래스
사이킷런의 결정 트리 구현은 CART(Classification And Regression Trees) 알고리즘을 기반으로 합니다.
주요 파라미터는 다음과 같습니다.
| 파라미터 | 설명 |
| min_samples_split | - 노드를 분할하기 위한 최소한의 샘플 데이터 수 |
| min_samples_leaf | - 말단 노드가 되기 위한 최소한의 샘플 데이터 수 |
| max_features | - 최적의 분할을 위해서 고려할 최대 피처의 개수 |
| max_depth | - 트리의 최대 깊이를 규정합니다. |
| max_leaf_nodes | - 말단 노드의 최대 개수 |
결정 트리 모델 시각화
Graphviz 패키지를 사용하면 결정 트리 알고리즘이 어떠한 트리로 구성되는지 시각화를 시킬 수 있습니다.
사이킷런에서는 Graphviz 패키지와 쉽게 인터페이스할 수 있도록 export_graphviz() 함수를 제공합니다.
붓꽃 데이터를 사용해서 시각화를 해보겠습니다.
In
from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
import warnings
warnings.filterwarnings('ignore')
dt_clf=DecisionTreeClassifier(random_state=156)DecisionTree Classifier를 생성해줍니다.
iris_data=load_iris()
X_train, X_test, y_train, y_test = train_test_split(iris_data.data,iris_data.target,
test_size=0.2, random_state=11)
dt_clf.fit(X_train, y_train)학습, 테스트 데이터 세트로 분리하여 학습시켜 줍니다.
from sklearn.tree import export_graphviz
export_graphviz(dt_clf,out_file="tree.dot",class_names=iris_data.target_names, \
feature_names=iris_data.feature_names, impurity=True, filled=True)
import graphviz
with open("tree.dot") as f:
dot_graph=f.read()
graphviz.Source(dot_graph)export_graphviz()에 인자로는 학습이 완료된 estimator, output 파일 이름, 결정 클래스의 이름, 피처의 이름을 입력해주면 됩니다.
Out
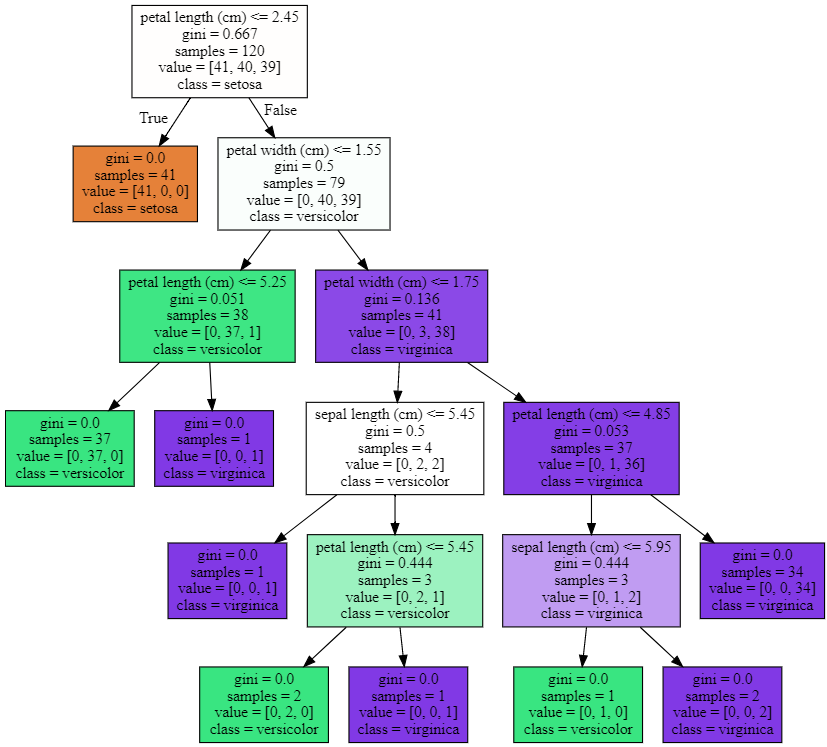
- petal length(cm) <= 2.45처럼 피처의 조건이 있는 것은 자식 노드를 만들기 위한 규칙 조건입니다.
- gini는 다음의 value=[]로 주어진 데이터 분포에서의 지니 계수입니다.
- samples는 현 규칙에 해당하는 데이터 건수입니다.
Reference
'Machine Learning' 카테고리의 다른 글
| 앙!상블 (0) | 2020.04.21 |
|---|---|
| 결정 트리 실습(사용자 행동 인식 데이터) (0) | 2020.04.19 |
| 사이킷런으로 시작하는 머신러닝 - 데이터 전처리(피처 스케일링)- (0) | 2020.04.10 |
| 사이킷런으로 시작하는 머신러닝 - 데이터 전처리(데이터 인코딩)- (0) | 2020.04.10 |
| 사이킷런으로 시작하는 머신러닝 - Model Selection 모듈(2)- (0) | 2020.04.09 |



